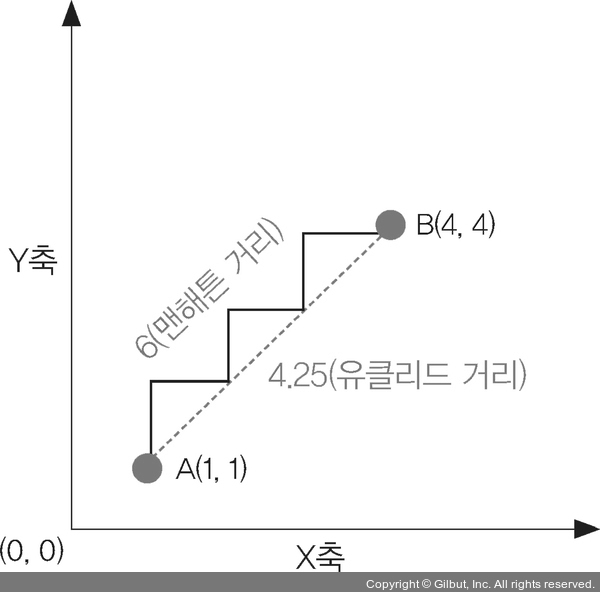
먼저 2차원 거리 측정 함수로 맨해튼거리(택시거리), 유클리드 거리 두 가지가 있다는 것을 알아두자.
교차점의 개수 세기
선분이 N개 있을 때, 교차점의 개수를 세는 문제이다. 이때 각각의 선분은 수평 선분이거나 수직 선분이다.
O(N^2)으로 쉽게 풀 수 있지만 스윕 라인 알고리즘과 구간 질의 자료 구조를 사용하면 O(NlogN) 시간에 풀 수 있다.
선분이 시작하는 점과 끝나는 점을 가지고 이벤트 처리하는 것이라고 생각하면 된다.
가장 가까운 점 쌍 찾기
점 N개가 있을 때 유클리드 거리가 최소인 두 점을 찾는 문제이다. 이 문제도 스윕 라인 알고리즘으로 O(NlogN) 시간에 해결할 수 있다.
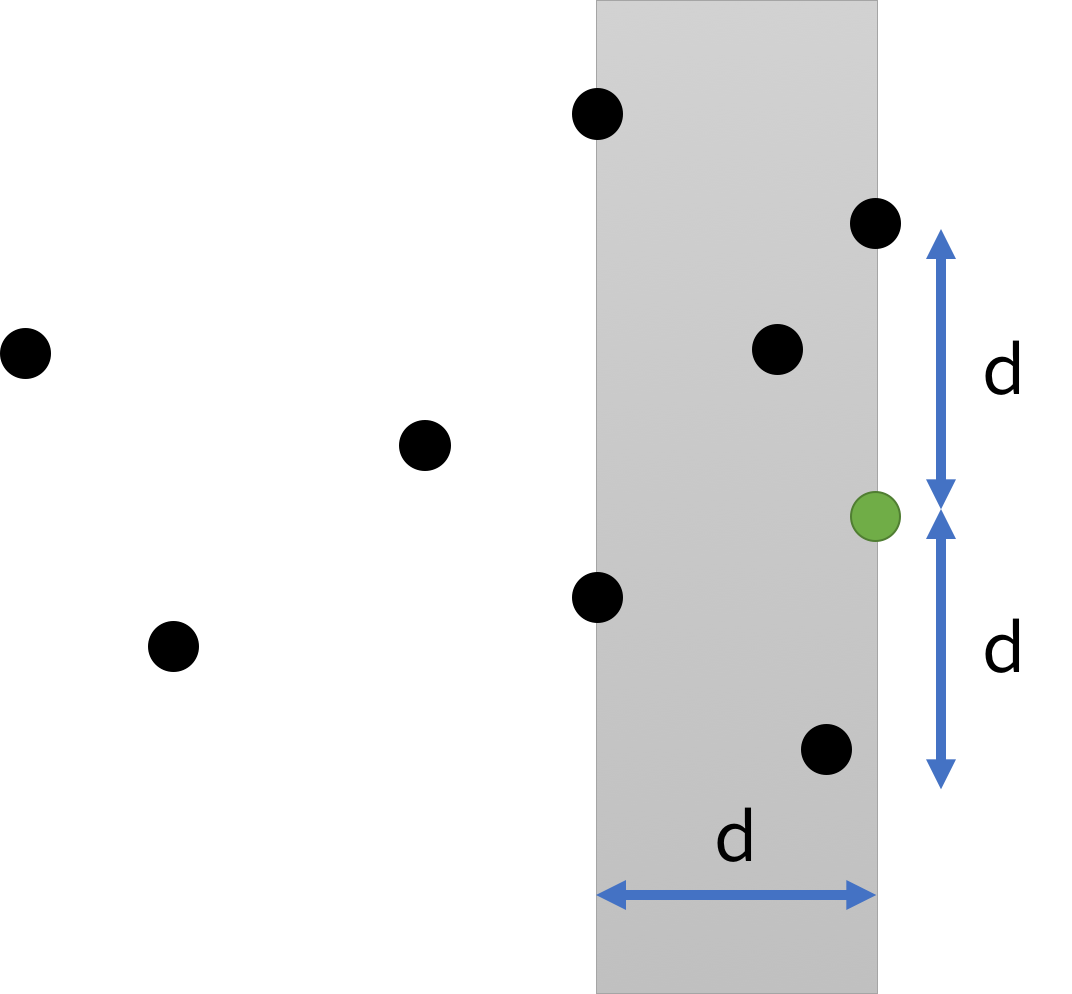
점들을 왼쪽에서 오른쪽 순서로 살펴보면서 d라는 값을 관리해 나간다.d는 현재까지 구한 두 점 사이의 최소 거리이다.
두 점 사이의 거리가 d보다 작다면, 새로운 최소 거리를 구한 것이므로 d값을 갱신한다. 현재 살펴보는 점이 (x, y)라면 거리가 d보다 가까운 점이 오른쪽에 있다고 하자. 그럼 그 점의 x좌표가 [x, x-d] 범위 사이에 있어야 하고, y좌표는 [y-d, y+d] 범위 내에 있어야 한다.
볼록 껍질
볼록 껍질(Convex hull)은 주어진 점을 모두 포함하는 가장 작은 볼록 다각형이다. (볼록하다는 의미는 다각형의 어느 두 꼭짓점을 택하더라도 그 둘을 연결하는 선분 전체가 다각형 내부에 놓여 있다는 뜻)
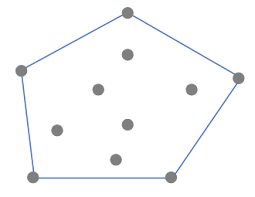
볼록 껍질을 구하는 알고리즘은 여러 가지가 있지만 그 중 가장 간단한 것이 앤드루 알고리즘이다.
앤드루 알고리즘
먼저 주어진 점들 중 가장 왼쪽 점과 오른쪽 점을 구하고, 두 단계로 나누어 볼록 껍질을 구해 나간다. 각 단계에서는 위쪽 껍질과 아래쪽 껍질을 구한다.
위쪽 껍질을 구하는 방법을 알아보자. 아래쪽 껍질을 구하는 방법도 이와 유사하다.

1. 점들을 x좌표 기준으로, 그 다음은 y좌표 기준으로 정렬한다.
2. 그 점을 껍질에 추가해본다.
→ 점을 껍질에 추가한 후에는 껍질의 마지막 선분이 왼쪽으로 회전하지 않는다는 성질을 항상 만족해야 한다.
3. 왼쪽으로 회전하는 선분이 생긴다면 제거하고, 그러지 않을 때까지 반복한다.
'컴퓨터공학 > 수학' 카테고리의 다른 글
| [기하] C++의 복소수 클래스 complex (0) | 2023.06.01 |
|---|---|
| [기하] 벡터와 외적의 활용 (0) | 2023.05.31 |
| [알고리즘] 분할정복으로 거듭제곱 최적화하기 (0) | 2023.05.30 |
| [정수론] 모듈러 연산과 증명 (0) | 2023.05.29 |
| [기하] 다각형 넓이 구하는 공식 (0) | 2023.05.28 |


