외적
기하문제에서 요긴하게 사용되는 외적을 이용해 알고리즘을 공부하자.
외적 배운 지 까마득 하지만.....🤣



우선 두 벡터의 외적 값 자체의 해석을 알아보자.

1. a x b > 0 : b는 왼쪽으로 회전한다.
2. a x b = 0 : b는 회전하지 않는다 또는 180도 회전한다 (a와 b가 평행하다.)
3. a x b < 0 : b는 오른쪽으로 회전한다.
점의 위치 판별하기
외적을 이용하면 어떤 점이 직선의 왼쪽 혹은 오른쪽 중 어느 곳에 있는지를 판별할 수 있다.
직선이 두 점 a, b를 지난다고 가정하자. 이때 방향이 a, b를 향하고 있고, 주어진 점은 p라고 하자.

(p - a) X (p - b)를 구하면 p의 위치를 알 수 있다. 외적이 양수라면 p가 선분 왼쪽에 있는 것이고, 외적이 음수라면 p가 선분 오른쪽에 있는 것이다. 그리고 외적이 0이면 a, b, p가 일직선 상에 있다.
선분 교차
또한 선분 ab와 cd가 교차하는지 여부를 판별할 수 있다.
첫 번째 경우 - 선분이 일직선 상에 있는 경우

외적을 이용하여 모든 점이 일직선 상에 있는지를 검사하면 된다. 만약 점들이 일직선 상에 있다면, x축 기준으로 정렬하여 두 선분이 서로 겹치는지를 검사한다.
회의실 문제 같은 그리디 문제도 따지고 보면 기하 문제다!
두 번째 경우 - 두 선분이 꼭짓점을 공유하는 경우

이런 경우는 쉽게 판별할 수 있다. 경우의 수가 a=c, a=d, b=c, b=d 네 가지 중 하나이기 때문이다.
세 번째 경우 - 꼭짓점이 만나지 않고 선분이 교차하는 경우

두 선분이 공통된 꼭짓점을 공유하지 않고 평행하지 않다면 교차한다. 점c가 선분ab를 지나는 직선 왼쪽에, 점d가 선분ab를 지나는 직선 오른쪽에 있는지 계산하면 판별할 수 있다.
점과 직선 사이의 거리
세 점이 이루는 삼각형의 넓이를 외적으로 구할 수 있다.
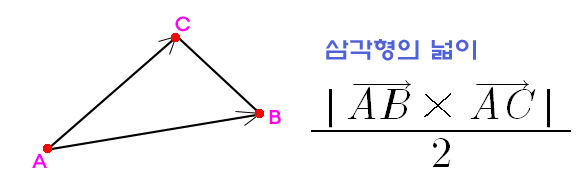
또한 삼각형 넓이 공식을 이용해 점과 직선 사이 거리 d를 구할 수 있다.
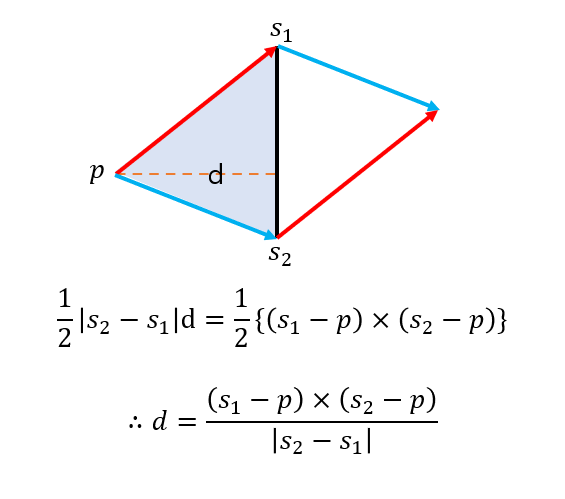
다각형 내부의 점, 외부의 점
주어진 점이 다각형의 내부와 외부 중 어느 쪽에 놓여 있는지를 판별하는 방법을 알아보자.
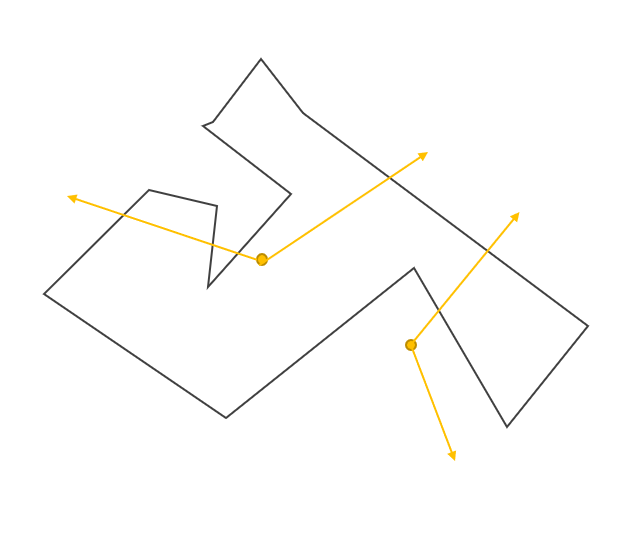
방법은 간단하다. 점에서 임의의 방향으로 선분을 긋고 선분이 다각형과 만나는 횟수를 세는 것이다. 횟수가 홀수라면 점이 다각형 내부에 있는 것이고, 짝수이면 외부에 있는 것이다.
이제 백준 플레 수학 문제를 정복하자^^!
'컴퓨터공학 > 수학' 카테고리의 다른 글
| [기하] 스윕 라인 알고리즘(교차점, 가까운 점, 볼록껍질) | 모르면 절대 못 품 (0) | 2023.06.02 |
|---|---|
| [기하] C++의 복소수 클래스 complex (0) | 2023.06.01 |
| [알고리즘] 분할정복으로 거듭제곱 최적화하기 (0) | 2023.05.30 |
| [정수론] 모듈러 연산과 증명 (0) | 2023.05.29 |
| [기하] 다각형 넓이 구하는 공식 (0) | 2023.05.28 |


