⚠️ 통계 하나도 모르는 주인장입니다.
ARIMA Model
ARMA 모델은 정상성이 있다는 것을 가정한 상황에서 사용하는 반면, ARIMA 모델은 차분이라는 개념을 통해 non-stationary한 상황에서 좀 더 나은 예측을 하는 것이 목표
따라서 ARMA모델에 차분이라는 차수 d가 포함되어 ARIMA(p,d,q)로 표현
- 차분 차수 d : 시계열 plot을 보고 정상성 여부를 확인하고, 차분을 진행하고, 차분 후의 plot을 보고 여부를 확인하는 프로세스로 진행한다.
- p, q : p, q의 경우 보통 ACF(Autocorrelation function)와, PACF(Partial Autocorrelation function)를 보고 결정한다. ACF는 k lag 단위로 구분된 시계열 관측치 X_t와 X_t-k 간의 상관 측도이고, PACF는 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열의 관측치X_t와 X_t-k 간의 상관 측도이다
ARIMA 모델 결과 및 검증
ADF (Augmented Dickey-Fuller Test)
시계열 데이터가 stationary 한지 확인하는 테스트. 안정적인 시계열 데이터는 통계적인 특성이 시간에 따라 변하지 않는 데이터를 의미합니다. 반면에 단위근이 존재하는 데이터는 추세나 계절성 등이 있어 시간에 따라 통계적 특성이 변하는 데이터를 의미한다. 귀무가설(Null hypothesis)이 기각되는지를 확인하는 지표이다.
귀무가설이란 두 모수치 사이에 차이가 없다고 하는 가설로, 기각될 것을 상정 하고 있다. 예를 들어 신약이 개발됐을 때 귀무가설은 ‘구약과 효과가 차이 없을 것이다’로 설정할 수 있다.
p-value
p-value는 귀무가설이 참일 때, 얻은 통계량 혹은 그보다 더 극단적인 통계량이 나올 확률을 의미한다. p-value가 낮을수록(0에 가까울수록) 귀무가설을 기각할 수 있는 강력한 증거가 된다
- 0.05보다 작으면 통계적으로 유의미하다고 판단
Critical Values(임계값)
귀무가설을 평가하기 위한 임계값으로, 귀무가설이 참일 때 얻을 수 있는 통계량의 임계값을 나타낸다. critical values보다 통게량이 작으면, 귀무가설을 충분히 기각할 통계적 근거가 있다고 판단된다.
- 1% 유의수준의 Critical Value가 가장 엄격하며 작다
- 5% 유의수준의 Critical Value는 중간 정도의 엄격성을 갖는다
- 10% 유의수준의 Critical Value는 상대적으로 덜 엄격하다
Critical Value와 ADF 통계량을 비교하여 결정하는데, ADF 통계량이 Critical Value보다 작다면 귀무가설을 기각할 충분한 통계적 증거가 있다고 판단할 수 있다
월평균 전력 소비량을 가지고 임의로 일일 전력 소비량 데이터를 만들었다. 전력 소비는 계절성을 가지고 있어 여름~늦가을까지 소비량이 많다.
ARIMA 모델에 적용할 p, d, q 값을 정해보자.
차수 d

위에서부터 Original, 1차차분, 2차차분 데이터에 따른 시계열 데이터이다.
이 데이터를 이용해 시계열 분석을 해 볼 것이다. 일단 차분을 적용하지 않은 Original 데이터이다.

파란색 - 원본 데이터
빨간색 - 이동 평균, 추세(기준 14일)
초록색 - 이동 표준 편차
시계열 데이터는 정상성을 가지지 않고, p-value가 0.05보다 커 귀무가설을 기각할 수 없다고 본다. 하지만 통계는 전체적인 값을 확인해야 되기 때문에 p-value가 크다고 해서 신뢰성이 떨어지지 않는다.
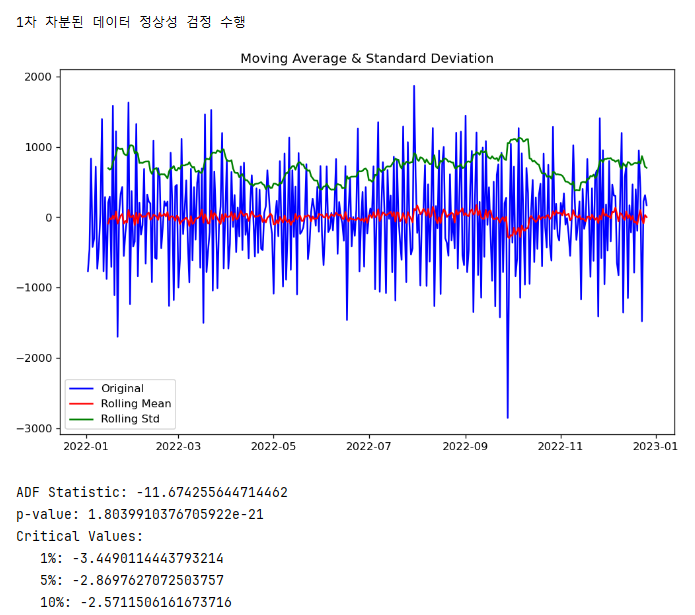
이번엔 1차 차분을 적용했다. 차분하지 않은 그래프보다 p-value가 매우매우매우 작아진 것을 확인할 수 있다. 그런데 critical values는 변하지 않았군?

2차 차분한 데이터는 ADF값도, p-value도 1차 차분 데이터보다 커졌다. 내 데이터는 1차 차분만 하는 게 더 적절해 보인다.
자기상관계수 p, 이동평균차수 q
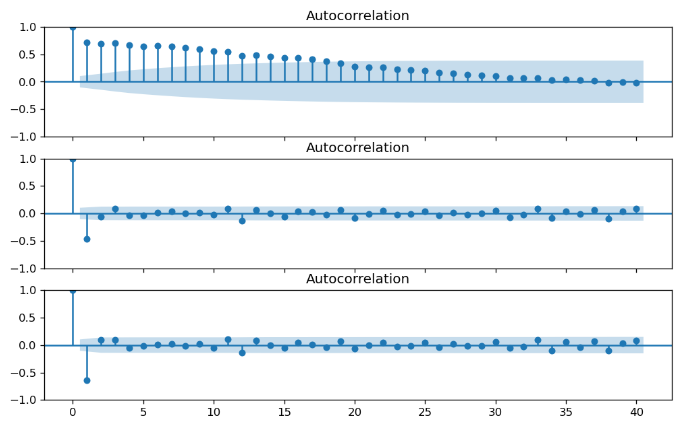
위에서부터 순서대로 Oringinal, 1차 차분, 2차 차분 ACF그래프이다.
먼저 자기상관 개념을 알아야 한다.
자기상관 (Autocorrelation)
데이터에서 다른 시점인데, 비슷한 상관관계가 나타나는 것을 의미한다. 예를 들어 전력 데이터는 여름철 에어컨 사용으로 봄-여름-가을-겨울) (평이-증가-감소-평이) 동향을 보이는데, 이는 1년 주기로 반복된다. 따라서 전력 데이터의 주기는 1년(365일)이다.
ACF (Autocorrelation Function)
시차k에 따라 나타나는 자기상관을 확인하는 그래프이다. t시점과 t-k시점(시차k) 데이터의 상관관계를 의미한다. 정상적 시계열일수록 0에 더 근접하다! 비정상 시계열은 Original ACF처럼 큰 수에서 감소하는 형태이다.
PACF (Partial Autocorrelation Function)
ACF에서 순수하게 t시점과 t-k시점 데이터 간의 상관관계를 파악하는 함수이다. 더 자세하게 말하자면, t-1, t-2, ... t-(k-1) 데이터는 무시하고 t, t-k만 고려한다.
→더 자세한 내용은 검색을 해주세요 저도 잘 모릅니다
N년치 데이터가 아닌 1년치 데이터기 때문에 자기상관성을 보이지 않는다. 여기 저기 찾아보니 신뢰구간에 있는 시차를ARIMA모델에 적용하는 것은 유의미하지 않다고 한다. 그래서 p=0로 지정했다.
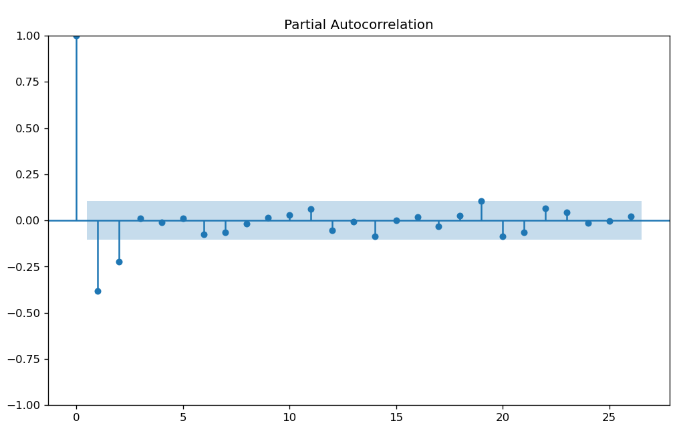
q도 마찬가지로 급격하게 감소하는 시차 이전 값을 q로 선택한다고 한다. q또한 1 또는 0으로 설정한다.
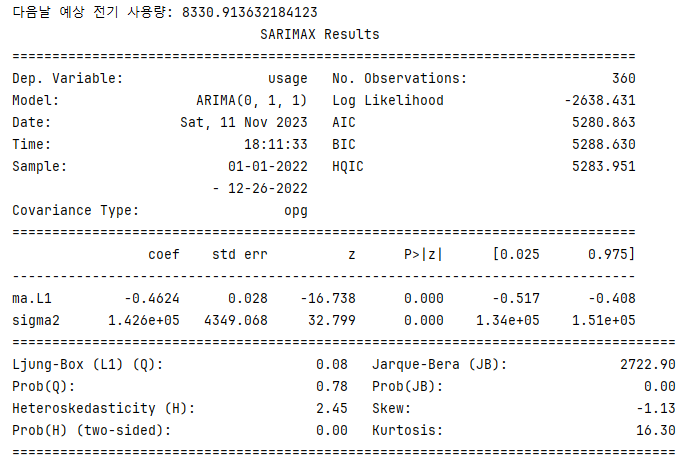
그렇게 도출된 결과이다.